Vanliga beräkningsmetoder för bågar är följande:
- Linjär knäckningsanalys.
- Andra ordningens analys.
Linjär knäckningsanalys
Linjär knäckningsanalys tillämpas på samma sätt som balk – pelare, det vill säga för samtidigt tryckta och böjda konstruktionsdelar. Spänningarna som förorsakas av de yttre lasterna beräknas med hjälp av linjär elasticitetsteori så att man bedömer jämvikten i det odeformerade statiska systemet. Spänningarna som förorsakas av geometriska avvikelser i bågens plan och tvärs bågens plan och de påförda deformationerna beaktas så att tryckhållfastheten och böjhållfastheten multipliceras med reduktionsfaktorerna som beaktar knäckning, kc och kcrit.
Tvåledsbågarnas knäckningsmod är alltid asymmetrisk oberoende av om lasten är symmetrisk eller osymmetrisk, se figur 11.15 b). Detta innebär att nocken flyttas i sidled i bågens plan och att böjmomentet byter tecken vid nocken. I fallet med en treledsbåge med relativt stort förhållande mellan pilhöjd och spännvidd (alltså f ⁄ l > 0,3) är knäckningen asymmetrisk även om lasten är symmetrisk, se figur 11.12 a).
När knäcklasten beräknas med hjälp av den förenklade analysen, behövs knäcklängden le. Den kan bestämmas antingen med hjälp av a) numerisk analys, till exempel linjär knäckningsanalys som utförs med hjälp av ett datorprogram som utnyttjar finita elementmetoden, eller med b) empiriska ekvationer.
Enligt Timoshenko et al. (1963) är det kritiska värdet för en jämnt fördelad last på en tvåleds eller en treleds parabelbåge med konstant tvärsnitt:
11.19 \({q_{\rm cr}} = \gamma \cdot \frac{{E \cdot I}}{{{l^3}}}\)
Den numeriska faktorn γ presenteras som en funktion av f ⁄ l i figur 11.13.
En cirkelbåge eller en parabelbåge med konstant tvärsnitt, förhållandet mellan pilhöjd och spännvidd f ⁄ l ≈ 0,15, längden av vardera båghalvan s samt lutningen αl ⁄ 4 i fjärdedelspunkten och som belastas med jämnt fördelad last visas i figur 11.14. Bågens knäcklast i fjärdedelspunkten Ncr enligt Eulers teori är given i figur 11.14.
(Observera att de geometriska storheterna i figur 11.14 är baserade på uttrycken givna i figur 11.5).
Det kritiska värdet för normalkraften i bågens fjärdedelspunkt är:
11.20 \({N_{{\rm cr},l/4}} \approx 1,04 \cdot \frac{{{q_{\rm cr}} \cdot {l^2}}}{{8 \cdot f}} = 1,04 \cdot \gamma \cdot \frac{{E \cdot I}}{{8 \cdot f \cdot l}}\)
När man jämför detta med Eulers kritiska kraft för en axiellt belastad pelare med längden s (= 0,53 · l):
11.21 \({N_{\rm cr}} = {\pi ^2} \cdot \frac{{E \cdot I}}{{{{\left( {\beta \cdot s} \right)}^2}}}\)
och avläser värdet γ ≈ 32 för f ⁄ l = 0,15 i figur 11.13, blir faktorn β för knäcklängden:
11.22 \(\beta = 1,17\)
Vid praktisk dimensionering antas ofta ett mera konservativt värde på knäcklängden le när man betraktar bågars knäckning i plan:
11.23 \({l_\rm e} = \beta \cdot s = 1,25 \cdot s\)
Det är uppenbart att osymmetriska lastfall, sådana som visas i figur 11.4, ger annorlunda knäcklängder än symmetriska lastfall. Vid preliminär dimensionering kan man ändå använda knäcklängden le = 1,25 · s även i det osymmetriska lastfallet, vilket för det mesta leder till resultat på den säkra sidan.
Dimensioneringsvillkoret beaktar samverkan av böjmoment och axialkraft och är:
11.24 \(\frac{{{\sigma _{\rm m,y,d}}}}{{{k_\rm r} \cdot {f_{\rm m,y,d}}}} + \frac{{{\sigma _{\rm c,0,d}}}}{{{k_{\rm c,y}} \cdot {f_{\rm c,0,d}}}} \le 1\)
där: kc,y är reduktionsfaktorn som beaktar knäckning i planet (alltså knäckning kring y-axeln, se figur 11.11) och de andra symbolerna som i ekvation 11.18 och avsnitt Raka balkar och pelare.
Icke-linjär analys
När belastningen ökar i en tryckt konstruktion ökar också deformationerna, och dessa ger större böjmoment som i sin tur ger större deformationer. Om man fortsätter öka belastningen leder denna process så småningom till att spänningen någonstans i konstruktionen överskrider materialets hållfasthet och därmed att brott uppstår. En geometrisk icke-linjär beräkning tar hänsyn till att moment (orsakat av tillskottsdeformationer) ökar med ökande axiallast. Om den icke-linjära beräkningen även tar hänsyn till strukturens initiella imperfektioner kommer resultatet att ge de ”riktiga” snittkrafterna. Dessa snittkrafter kan användas direkt för dimensioneringen, utan behov av att manipulera dessa med eventuella reduktionsfaktorer för knäckning (det vill säga k-faktorer). Dimensioneringen utförs därmed genom att kontrollera tvärsnittet för samtidig tryck och böjning utan hänsyn till risk för knäckning (det vill säga genom att sätta reduktionsfaktorn för knäckning till kc = 1,0).
Detta sätt att dimensionera en träkonstruktion är otänkbart utan användning av lämpliga finita elementprogram. Sådana program finns nu på marknaden och hur till exempel de geometriska imperfektionerna bör hanteras beror i viss mån på vad det aktuella programmet erbjuder för modelleringsmöjligheter. Ofta är den första eller den andra knäckningsmoden en god approximation för formen på den initiella imperfektionen, se figur 11.15. Alternativt kan man använda deformationerna som erhålls ur en linjärelastisk analys med aktuellt lastfall som indata för de initiella imperfektionerna i strukturen. Typiskt värde på imperfektionens maximala amplitud vid beräkning av limträkonstruktioner är cirka L / 400 enligt Eurokod 5 (se figur 5.3 i SS-EN 1995-1-1).
Förenklad icke-linjär analys (här av andra ordningen)
För bågar som har en initialformavvikelse som är likartad med någon av de lägsta knäckningsmoderna ger följande enkla approximativa ekvation en bra uppskattning på hur storleken för initialformavvikelse δ0 ökar på grund av andra ordningens effekter, se ekvation 4.19:
11.25 \({\delta _{\rm tot}} = {\delta _0} + {\delta _\rm p} = \frac{{{\delta _0}}}{{1 - H/{H_{\rm cr}}}}\)
där H är den ifrågavarande horisontalkomponenten av huvudlastkombinationen och Hcr är det kritiska värdet för H för den aktuella knäckningsmoden.
Böjmomentet M0 enligt den linjära teorin ökar med samma förstoringsfaktor som ovan till:
11.26 \({M^{II}} = \frac{{{M_0}}}{{1 - H/{H_{\rm cr}}}}\)
där M II är böjmomentet enligt andra ordningens teori. Ekvation 11.26 ger den bästa uppskattningen när böjmoment M0 har samma form som böjmomentet vid knäckning.
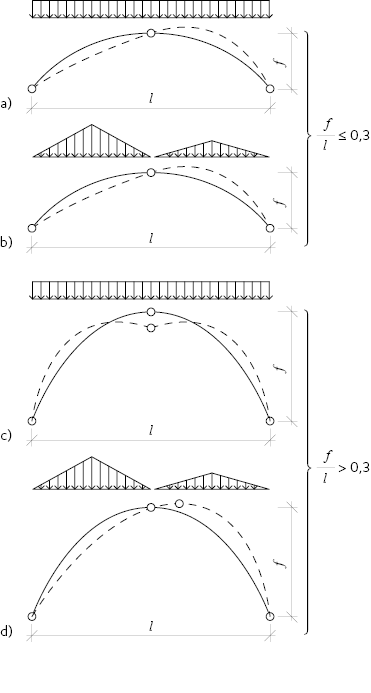
Figur 11.12 Treledsbågars knäckning i plan.
a) och b) gäller för f / l ≤ 0,3.
c) och d) gäller för f / l > 0,3.
För lastfall d) kan antingen en symmetrisk eller en assymetrisk knäckningsmod inträffa.
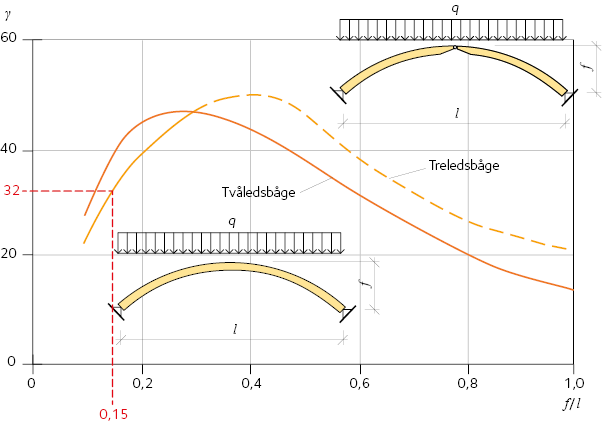
Figur 11.13 γ-värden som funktion av f ⁄ l. Den streckade delen av grafen motsvarar den symmetriska knäckningsmoden.
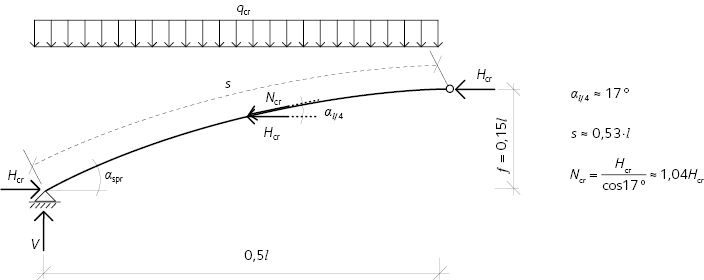
Figur 11.14 Krafterna som verkar i ena båghalvan av en treledsbåge. αl ⁄ 4 är vinkeln mellan bågens systemlinje och en horisontal linje i fjärdedelspunkten. s är längden av båghalvan. Ncr är knäcklasten enligt Eulers teori i bågens fjärdedelspunkt.
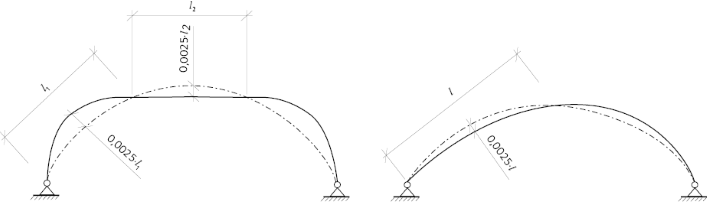
Figur 11.15 Rekommenderade antagna initialdeformationer enligt Eurokod 5.
a) Symmetrisk (antagen) initial deformation, likartad med den andra knäckningsmoden av en tvåledsbåge,
b) osymmetrisk (eller sidoförskjuten) initial deformation, likartad med den första knäckningsmoden.

Kolmårdens djurpark.

