Observera att knäcklängden beror på det valda stagningssystemet och i viss mån på takkonstruktionen. Till exempel kan en tillräckligt styv takskiva, som profilerad plåt fastskruvad i rambalken, förhindra knäckningen ut ur ramens plan. Om den styva takplåten är fastskruvad i takåsarnas övre kant, kan knäckning ut ur planet ske mellan de punkter där takåsarna är fastsatta i rambalken (knäcklängden är då a1, se figur 10.4). Om takskivan inte är tillräckligt styv, som till exempel en cementbunden spånskiva eller motsvarande, bör knäcklängden som används vid dimensionering väljas till avståndet mellan vindfackverkets knutar (knäcklängden är då a, se figur 10.4).
Rambalkens knäckning ut ur plan
Knäckning ut ur ramens plan ska kontrolleras i de icke stagade områdena på samma sätt som för tryckta balkar, enligt modellen som visas i figur 10.5.
Dimensioneringsvillkoret är:
10.7 \(\left\{ \begin{array}{l} {\left( {\frac{{{\sigma _{\rm m,y,d}}}}{{{k_{\rm crit}} \cdot {f_{\rm m,y,d}}}}} \right)^2} + \frac{{{\sigma _{\rm c,0,d}}}}{{{k_{\rm c,z'}} \cdot {f_{\rm c,0,d}}}} \le 1\\ \frac{{{\sigma _{\rm c,0,d}}}}{{{k_{\rm c,z'}} \cdot {f_{\rm c,0,d}}}} + {k_\rm m} \cdot \frac{{{\sigma _{\rm m,y,d}}}}{{{f_{\rm m,y,d}}}} \le 1 \end{array} \right.\)
där:
| σc,0,d | är dimensioneringsvärdet för tryckspänningen parallellt fibrerna. |
| σm,y,d | är dimensioneringsvärdet för böjspänningen kring y-axeln. |
| fc,0,d | är dimensioneringsvärdet för tryckhållfastheten parallellt fibrerna. |
| fm,y,d | är dimensioneringsvärdet för böjhållfastheten kring y-axeln. |
| kc,z' | är reduktionsfaktorn som beaktar knäckning ut ur planet (alltså kring z'-axeln, se figur 10.4). |
| kcrit | är reduktionsfaktorn som beaktar vippning, se avsnitt 4.1.3. |
| km | är en faktor som beaktar omfördelning av spänningar och inverkan av inhomogeniteter i materialets tvärsnitt. Den antar värdet 0,7 för rektangulärt tvärsnitt. |
För mer detaljerad information om de använda beteckningarna, se också avsnitt Raka balkar och pelare.
De krökta delarnas knäckning ut ur plan
Vanligtvis stagas ramarna inte i området vid ramhörnet. Tyngdkraften förorsakar negativa böjmoment vid hörnet vilket medför tryckspänningar i tvärsnittets underkant. Därtill förekommer tryckspänningar förorsakade av normalkraften i detta område. Därför ska ramhörnet kontrolleras för samtidig tryck och böjning. Dimensioneringsvillkoren som ska uppfyllas är desamma som för rambalken, se ekvation 10.7, med undantag för koefficienten kr, se avsnitt Snedsågade balkar, krökta balkar och bumerangbalkar, som beaktar att hållfastheten reduceras på grund av att lamellerna kröks vid tillverkningen.
10.8 \(\left\{ \begin{array}{l} {\left( {\frac{{{\sigma _{\rm m,y,d}}}}{{{k_{\rm crit}} \cdot {k_\rm r} \cdot {f_{\rm m,y,d}}}}} \right)^2} + \frac{{{\sigma _{\rm c,0,d}}}}{{{k_{\rm c,z'}} \cdot {f_{\rm c,0,d}}}} \le 1\\ \frac{{{\sigma _{\rm c,0,d}}}}{{{k_{\rm c,z'}} \cdot {f_{\rm c,0,d}}}} + {k_\rm m} \cdot \frac{{{\sigma _{\rm m,y,d}}}}{{{k_\rm r} \cdot {f_{\rm m,y,d}}}} \le 1 \end{array} \right.\)
Vid beräkning av det kritiska böjmomentet Mcrit som används vid bestämning av det motsvarande slankhetstalet och reduktionsfaktorn kcrit, se avsnitt 4.1.3, bör följande ekvation användas:
10.9 \({M_{\rm crit}} = \frac{\pi }{{{s_0}}} \cdot \sqrt {\left( {E \cdot {I_\rm z}} \right) \cdot \left( {G \cdot {k_\rm v}} \right)} + \frac{{\left( {E \cdot {I_\rm z}} \right) + \left( {G \cdot {k_\rm v}} \right)}}{{2 \cdot r}}\)
där:
\({I_\rm z} = \frac{{{b^3} \cdot h}}{{12}}\)
och:
\({k_\rm v} = \frac{{{b^3} \cdot h}}{3} \cdot \left( {1 - 0,63 \cdot \frac{b}{h}} \right)\)
där kv är vridstyvhetens tvärsnittsfaktor.
Observera att när r → ∞, blir ekvation 10.9 identisk med ekvationen för det kritiska böjmomentet för raka konstruktionsdelar utsatta för konstant böjmoment, se avsnitt Raka balkar och pelare.
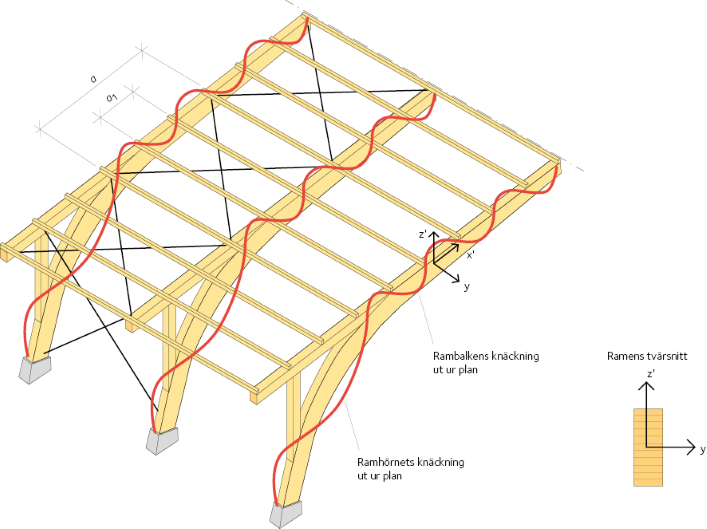
Figur 10.4 Ramens och ramhörnets knäckning ut ur plan. Taksystemet består av ett styvt skivmaterial, till exempel av profilerad plåt.

Lysingsbadet, Västervik.
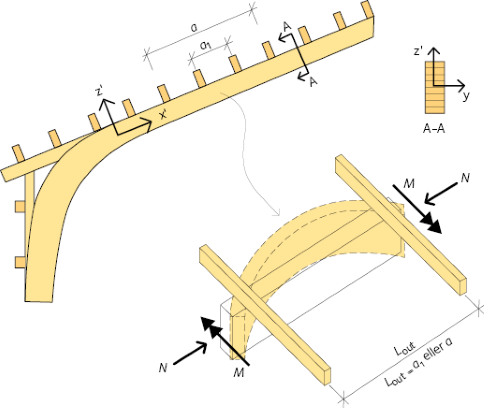
Figur 10.5 Modell för att kontrollera rambalkens knäckning ut ur plan. Om takmaterialet är tillräckligt styvt kan knäcklängden antas vara a1. I annat fall ska knäcklängden antas vara a, se också figur 10.4.
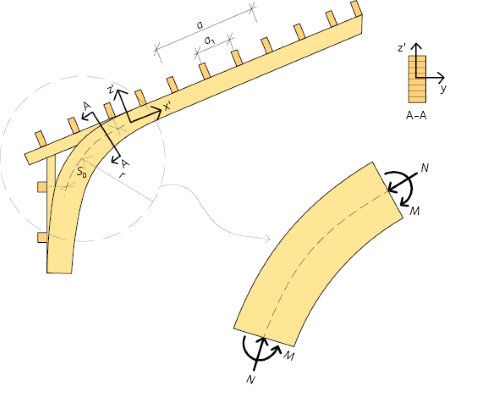
Figur 10.6 Modell för att kontrollera ramhörnets knäckning ut ur plan.

