Raka jämnhöga balkar
Ekvationer för beräkning av jämnhöga raka balkars nedböjning förorsakad av böjmoment finns i de flesta dimensioneringstabeller.
Om förhållandet L ⁄ h för balken är mindre än 10 bör skjuvdeformationer beräknas i tillägg till böjdeformationer; i annat fall kan de ignoreras.
För fritt upplagda balkar belastade med jämnt fördelad last är nedböjningen i mitten av spannet:
6.17 \({w_\rm m} = \frac{{5q{L^4}}}{{384EI}}\)
där index m indikerar nedböjning förorsakad av böjmoment. Nedböjningen av skjuvning är i detta fall:
6.18 \({w_\rm s} = \left( {1 + 0,96\left( {\frac{E}{G}} \right){{\left( {\frac{h}{L}} \right)}^2}} \right) \cdot {w_\rm m}\)
där index s indikerar nedböjning förorsakad av tvärkrafter. För både elasticitestsmodulen E och skjuvmodulen G bör medelvärdena användas.
För kontinuerliga balkar är nedböjningen i regel inte kritisk. Den största nedböjningen förekommer vanligtvis i ändfacken.
Raka balkar med linjärt varierande höjd
Pulpetbalkars och sadelbalkars nedböjning beräknas enklast med dimensioneringsprogram. Manuell beräkning med arbetsekvationer innebär en ansenlig mängd räknande. För fritt upplagda pulpetbalkar eller symmetriska sadelbalkar belastade med jämnt fördelad last kan nedböjningen i mitten av spannet uppskattas med hjälp av ekvationen:
6.19 \(w = \frac{{5q{L^4}}}{{384E{I_\rm e}}} + 0,35\frac{{q{L^2}}}{{Gb\left( {{h_\rm s} + {h_{\rm max}}} \right)}}\)
där:
| Ie | = bhe3 ∕ 12. |
| he | = hs + 0,33L · tan α för sadelbalkar. |
| he | = hs + 0,45L · tan α för pulpetbalkar. |
| hmax | = hap för sadelbalkar och hl för pulpetbalkar. |
För balkar med 2L ⁄ (hs+hmax) > 25 kan den andra termen i den föregående ekvationen ignoreras. Termen representerar inverkan av skjuvdeformationen.
För noggrannare beräkningar kan följande ekvationer och siffervärden användas, Jack Porteous & Abdy Kermani (2007).
Pulpetbalk med en koncentrerad last P i mitten av spannet:
6.20 \({w_\rm m} = \frac{{5M{L^2}}}{{96E{I_{{\rm h_\rm s}}}}}{k_{\rm 1\delta b}}\quad {\rm{med}}\quad M = \frac{{PL}}{4}\)
6.21 \({w_\rm s} = \frac{{1,2M}}{{G{A_{{\rm h_\rm s}}}}}{k_{\rm 1\delta s}}\)
Pulpetbalk med jämnt fördelad last:
6.22 \({w_\rm m} = \frac{{5M{L^2}}}{{48E{I_{{\rm h_\rm s}}}}}{k_{\rm 2\delta b}}\quad {\rm{med}}\quad M = \frac{{q{L^2}}}{8}\)
6.23 \({w_\rm s} = \frac{{1,2M}}{{G{A_{{\rm h_\rm s}}}}}{k_{\rm 2\delta s}}\)
Sadelbalk med en koncentrerad last i mitten av spannet:
6.24 \({w_\rm m} = \frac{{5M{L^2}}}{{96E{I_{{\rm h_\rm s}}}}}{k_{\rm 3\delta b}}\quad {\rm{med}}\quad M = \frac{{PL}}{4}\)
6.25 \({w_\rm s} = \frac{{1,2M}}{{G{A_{{\rm h_\rm s}}}}}{k_{\rm 3\delta s}}\)
Sadelbalk med jämnt fördelad last:
6.26 \({w_\rm m} = \frac{{5M{L^2}}}{{48E{I_{{\rm h_\rm s}}}}}{k_{\rm 4\delta b}}\quad {\rm{med}}\quad M = \frac{{q{L^2}}}{8}\)
6.27 \({w_\rm s} = \frac{{1,2M}}{{G{A_{{\rm h_\rm s}}}}}{k_{\rm 4\delta s}}\)
Krökta balkar
Krökta balkars deformationsberäkningar är komplicerade, men följande ekvationer kan användas för att uppskatta deformationerna:
6.28 \(w = \frac{{{w_\rm q}}}{{\left( {\cos \frac{{\alpha + \beta }}{2}} \right)}}\)
Här är wq den beräknade nedböjningen för en symmetrisk sadelbalk som har samma spännvidd och samma tvärsnitt vid stöden och i mitten av spannet som den krökta balken, se avsnitt Snedsågade balkar, krökta balkar och bumerangbalkar.
Den horisontella förskjutningen vid det ”fria” upplaget kan uppskattas med ekvationen:
6.29 \({w_\rm h} = 4\frac{{\left( {f + 0,8h} \right)}}{L}w\)
där:
| f | = vertikalt avstånd mellan neutralaxeln vid upplaget och nocken. |
| h | = balkhöjd vid upplaget. |
| L | = spännvidd. |
| w | = vertikal nedböjning i mitten av spannet. |
Fackverk
Limträfackverks deformationsberäkningar är mera komplicerade än enskilda balkars, eftersom både limträdelarna och förbanden deformeras. En uppskattning av nedböjningen i ett parallellfackverk, utan att förbandens deformationer beaktas, får man genom att beräkna nedböjningen för en massiv balk med tröghetsmomentet:
6.30 \(I = \sum {{A_\rm i}} \cdot {a_\rm i}^2\)
där:
| Ai | = respektive ramstångs tvärsnittsarea. |
| ai | = avståndet mellan respektive ramstångs tyngdpunkt och hela fackverkets tyngdpunkt. |
Eftersom förbanden är eftergivliga, är deformationerna i fackverk större än i massiva balkar. Ett problem är att ökningen av nedböjningen beror på antalet förband och förbandstypen. Mätningar har visat att nedböjningen kan öka med 10 – 15 procent jämfört med förband utan deformationer. Detta värde avser deformationsökning efter ett antal år. Förband med tandbrickor ger den minsta deformationen medan förband med spikade plywoodskivor ger större deformationer.
Därför rekommenderas att fackverk tillverkas med en överhöjning (både över- och underramen) som är ungefär L ⁄ 150 om L ⁄ h = 12 och L ⁄ 200 om L ⁄ h = 10.
Treledstakstolar
Treledstakstolars takbärande konstruktion består vanligtvis av överramar av limträ och dragband som antingen är av limträ eller av stål.
Den vertikala nedböjningen av jämnt fördelade nedåtriktade laster enligt figur 6.8, kan beräknas med hjälp av ekvationen:
6.31 \(w = \frac{{\left( {{q_1} + {q_2}} \right){L^2}}}{{16{{\left( {\tan \alpha } \right)}^2}{{\left( {EA} \right)}_{\rm beam}}}}\left( {\frac{1}{{{{\left( {\cos \alpha } \right)}^3}}} + \frac{{{{\left( {EA} \right)}_{\rm beam}}}}{{{{\left( {EA} \right)}_{\rm tie}}}}} \right)\)
Om stöden är oeftergivliga är den andra termen inom parentesen lika med noll.

Kolmårdens djurpark.
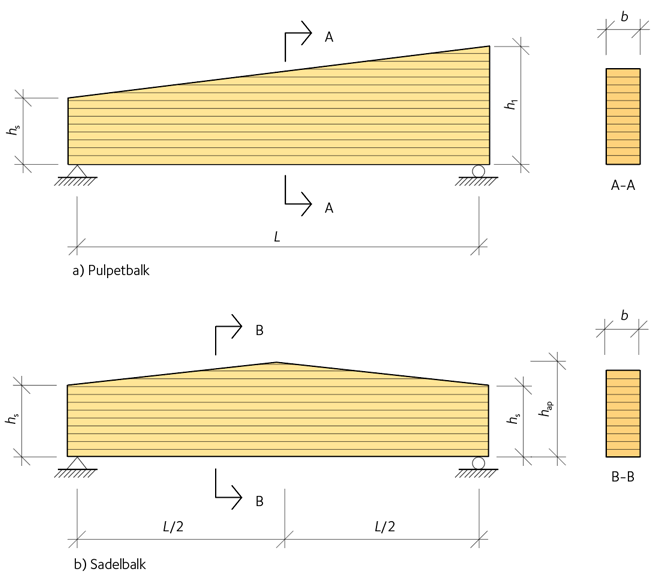
Figur 6.4 Pulpet- och sadelbalk.
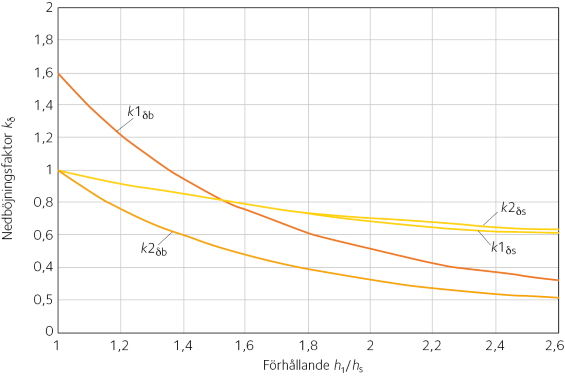
Figur 6.5 Värden på kδb och kδs för pulpetbalkar.
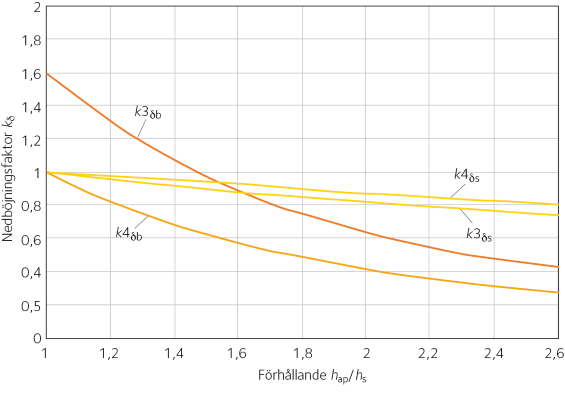
Figur 6.6 Värden på kδb och kδs för sadelbalkar.
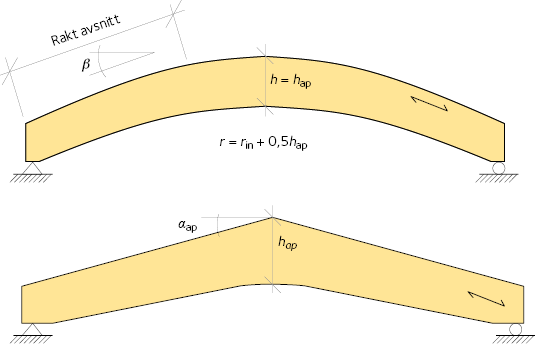
Figur 6.7 Krökt balk (övre figur) och bumerangbalk (nedre figur).
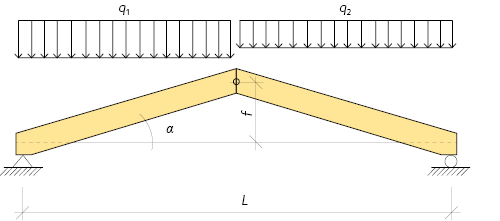
Figur 6.8 Treledstakstol med enkla takbalkar och ett dragband.

